Someone was looking to set up some LED panels, and I insisted they should form an icosahedron net for no particular purpose, as is my wont. Long story short, I tricked myself into learning a few things.

So the challenge was on to lay out a decent-looking set of triangles that could fold into an icosahedron, even though they would obviously never ever be folded into an icosahedron. Priorities, you know; this stuff matters.
You’ve no doubt seen the usual arrangement, a line of ten triangles with ten more along the top and bottom. But it doesn’t look very interesting nor exciting.
This sort of spatial geometry is far too much for my poor brain to handle, especially without any physical icosahedra to admire, so the first attempt was neither particularly appealing nor, on closer inspection, did it form an actual icosahedron. Oops.

It’s so obviously wrong, right? I couldn’t tell without deleting pieces step-by-step from the same 3D model that was supposed to be its basis, demonstrating the clear flaws in this haphazard methodology. Perhaps marginally deterred, I scrolled slightly further down through image search results for “icosahedron net,” and here’s where things start getting interesting.
Part of Figure 14 here shows a remarkably spaced-out, non-branching net:
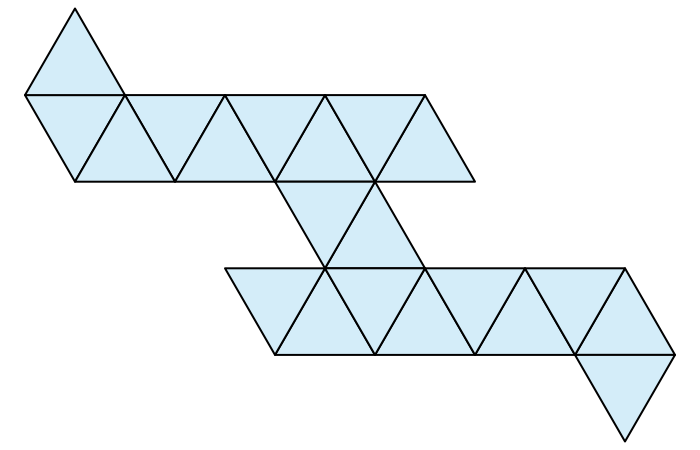
But the net from this page blew my mind:
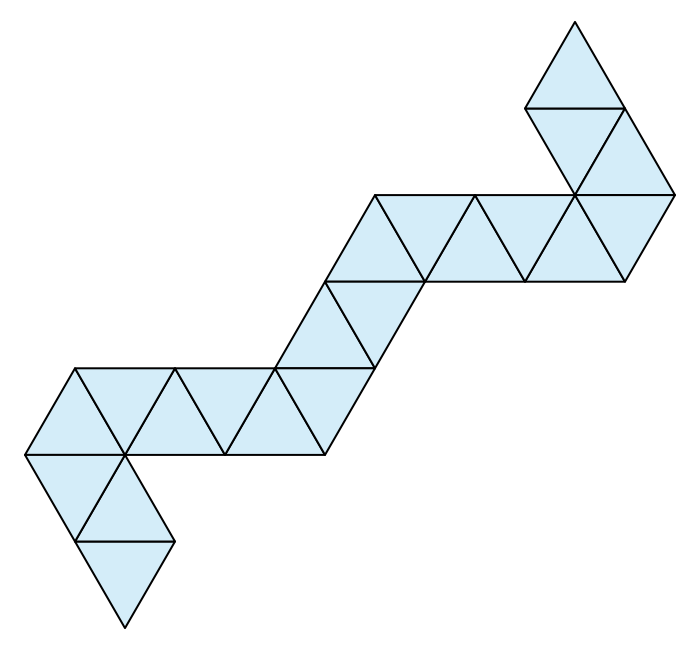
It’s a… completely non-branching path. Is that actually doable? It’s remarkably similar to the original concept, almost as though the pointless icosahedron needn’t even be a detraction. Some more advanced analysis is clearly going to be needed.
If the goal is to find some unbranching path across faces of an icosahedron, well, that’s kinda like (read: “is”) a Hamiltonian path in a graph of icosahedron faces. And with that done, maybe there could even be a complete cycle?
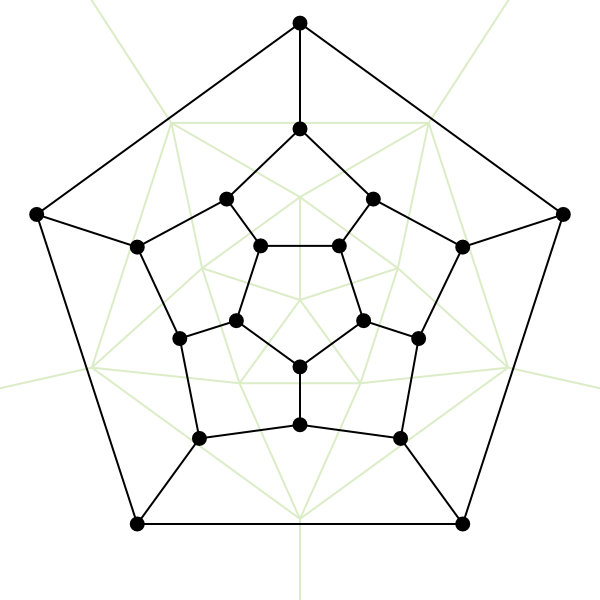
The vertices (black dots) of this graph are actually connected in the same way as the vertices of a dodecahedron – you can see the pentagonal faces formed by them. In fact the graph itself is called the “Dodecahedral graph.” So why is it here for an icosahedron? The icosahedron and dodecahedron have a special status as “duals”: the faces of each correspond exactly to the vertices of the other, with the same number of edges on both. The same relation holds for the cube and octahedron, while the dual of a tetrahedron is another tetrahedron: four faces and four vertices, each connected to the three others. The end result is, a graph of icosahedron faces will be the vertices of its dual (a dodecahedron), by the definition of dual.
So there’s a graph! Let’s see if we can make our own unbranching path through it.
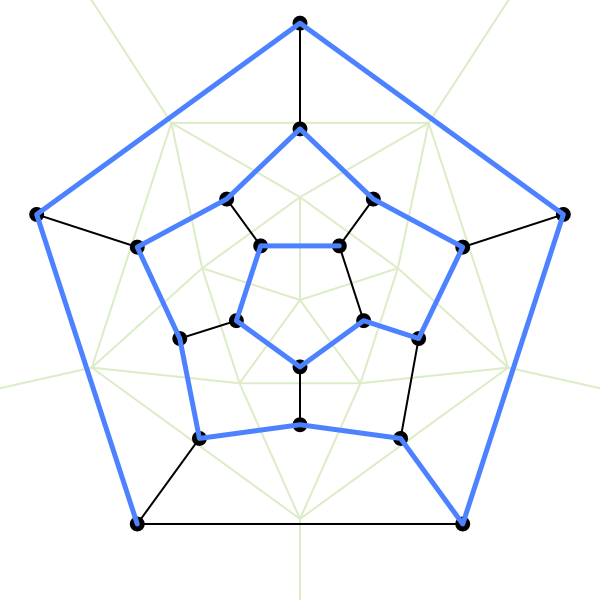
With a bit of effort, the net this is supposed to abstractly represent can be found. Mostly I try to keep track of where it turns “left” or “right,” which is a bit of a head-spinner but at least consistently doable.
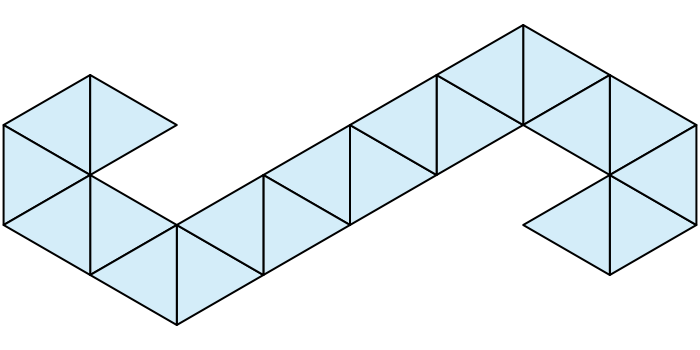
And that’s an icosahedron? In retrospect it seems obvious – there’s a line of ten triangles with caps of five more on each side. I find it quite remarkable how much easier this is to work with from a graph.
And finally, a complete cycle can indeed be found, though for a net it must be severed at some arbitrary point.
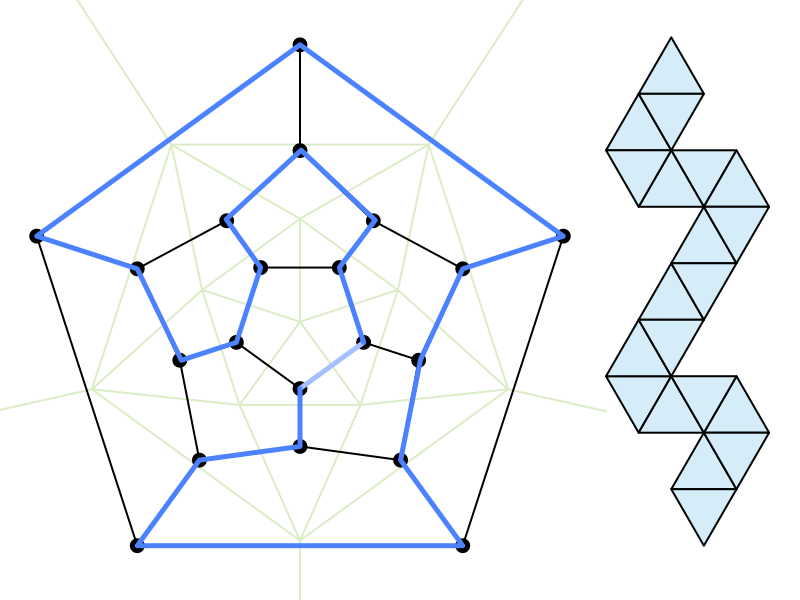
And this does form a real icosahedron! I ruled it out on paper and taped the ends together just for confirmation. Apparently finding a Hamiltonian cycle on the dodecahedral graph specifically is called the “icosian game.” Never heard of it before, but it’s evidently not too difficult to pull off… David Darling notes “the game was a complete sales flop, mainly because it was too easy, even for children.”
Of note is that, as far as I can tell, all Hamiltonian cycles for the dodecahedral graph are isomorphic (or whichever term the graph nerds/pedants would prefer). So any continuous cycle will yield nets that look like the image above, with some segment cut from the left and moved to the right. I chose to split it somewhere that gives a nice rotational symmetry.
So who cares about wall ornaments, here are some takeaways that I might have pulled from my arse, so be cautious: anything involving designing nets (a regular concern for many) is far easier if you first construct a graph of face connections, i.e. the dual of the polyhedral graph. Any net will then correspond to a “spanning tree” of the graph, a subgraph that includes every vertex (here representing faces) with no cycles. I guess.
Just to wrap up, a net where each face is as close as possible to a central one, using the techniques developed above:
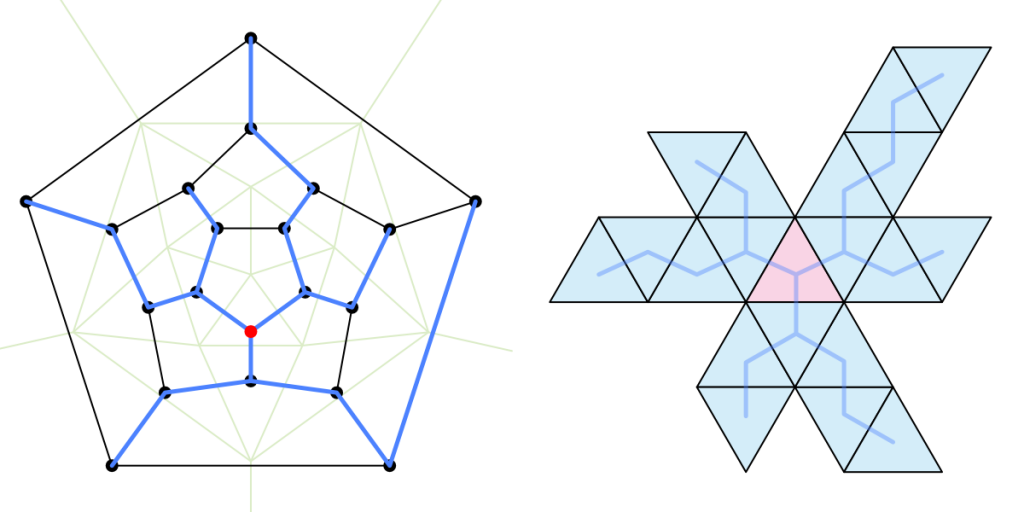
And one more thing… I noticed making these that there were always 10 triangles in one orientation and 10 in the reverse (for nets that are actually valid icosahedra, ahem…). But looking at the “standard” net, it seems trivial enough to move one or more of the top triangles into positions where they would be reversed, so the ratio would be unequal. I see such possibilities in other nets too. Is there some really funky graph theory that could indicate/predict the ratio? Evidently something to do with how far each vertex is from some arbitrary reference, since the triangles alternate orientation with each successive edge. What sort of graph would give the largest imbalance?
No comments found.