A story going around at the moment is how Microsoft Exchange ran into a problem with the new year – somewhere the time was being stored as an integer that reads in base 10 like YYMMDDHHMM, so once YY became 22 it exceeded the maximum of 2147483647 available to a signed 32-bit integer, drama ensued.

That’s the story I’ve read, anyway, but the details aren’t important. What matters is that this format is a horribly inefficient way to store that kind of data. Computers and integers don’t care about base 10 and you shouldn’t warp stuff into it for no reason.

The most efficient format for this kind of data is in the vein of Unix timestamps – count the number of seconds or days or [desired resolution] since a particular time, and there’s your integer. It’s guaranteed to map every single integer in the range to a complete, unbroken interval of time.

Problem is it’s harder to process. Thanks to the complications of calendars and convoluted methods of timekeeping, extracting even just the year from “1640955600 seconds since 1970-01-01 00:00 UTC” is not straightforward. Fortunately people with far more time to worry about these intricacies than us have already made libraries to deal with all of it, so I must preface (midface?) all of this with “just use the standard libraries,” and ask that you just keep the principles in mind when considering squeezing a bunch of stuff into one integer.

Throwing all that aside, what if we had the worst of both worlds, not optimally compact but also requiring more processing to extract?

(Exaggerating for comedic effect, what follows is honestly no harder to work with than the woefully inefficient method)

Packing a date

Dates in the Gregorian calendar have years of 12 months with 28–31 days. News to anyone no doubt. The (or, “A”) problem with squeezing a bunch of numbers together so it reads like 220103 is it wastes a lot of potential values. While a year has at most 366 days, this format distinguishes between 10000 days for any year – 96% of the potential values are wasted.

That’s because it’s been arbitrarily smashed to work nicely in base 10: Year × 10000 + Month × 100 + Day. A far better approach is hopefully apparent: multiply each part by only what is needed to distinguish them. Year × 12 + Month will uniquely encode any combination of year and one of 12 months. Even if one of those months is encoded as “12,” there won’t be a 0 for it to conflate with and just needs a but more processing to extract than if it were 0–11.

The only reason this approach will differ from the counting method of Unix timestamps is because months have differing numbers of days. And, with further resolution, sometimes days have different numbers of seconds. But leaving room for any month to potentially have 31 days, an efficient integer has the following format:

(Year × 12 + Month) × 31 + Day = Year × 372 + Month × 31 + Day

To simplify decoding, ensure months are from 0 to 11 and days from 0 to 30, and the date is far more compact. This can be done by the encoding operation as Year × 372 + Month × 31 + Day − 32, as −32 removes both one day and one month.

Today, 2022-01-03, becomes 752186, or just 8186 if the year is given as 22 instead of 2022. From 220103 to 8186 – it’s an obvious improvement with no sophisticated processing. This way every year distinguishes between 372 different days, which is more than the actual average of 365.2425 but literal orders of magnitude better than 10000.

Now to extract the individual values again just requires some simple integer division and remainder arithmetic.

Year = floor( datestamp / 372)
Month = floor[ ( datestamp mod 372 ) / 31 ] + 1
Day = ( datestamp mod 31 ) + 1

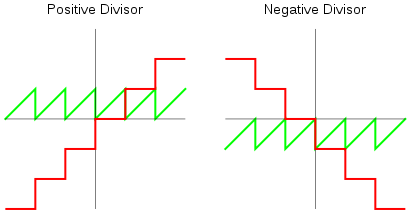
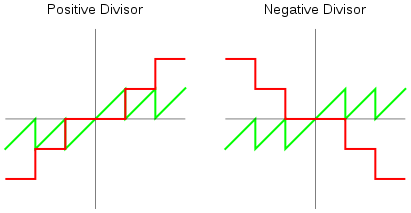
This will work as is even with negative years, so long as your language of choice implements modulo “correctly”, i.e. with the same sign as the divisor. JavaScript gets this wrong.

• 

• 

Datetimes

Working with days of the month is a bit odd. From here it’s straightforward, with days of exactly 24 hours from 0 to 23, and hours of 60 minutes from 0 to 59. Incorporating 60 seconds would be more of the same, but at that point you really should just be using normal timestamps anyway. More so than you already should be, that is.

Datetime = ( Year × 372 + Month × 31 + Day ) × 1440 + Hour × 60 + Minute

Equivalent to a final monstrosity,

Year × 535680 + Month × 44640 + Day × 1440 + Hour × 60 + Minute

Now the first minute of year “22” is merely 11784960, which is 182 times smaller than 2147483647. This method is so much better, that the year can literally be “2022” and still be going strong. In fact, this can encode every minute of every day of every year all the way up to and including year 4008. It gets all of year −4008, too.

The fundamental format of this encoding is no different than the atrocity that started all of this. It just doesn’t have an unwarranted devotion to base 10.