You may not know it, but all logic gates can be made from NOT and OR gates alone. So, I set out to make them!
First of all, the AND gate:
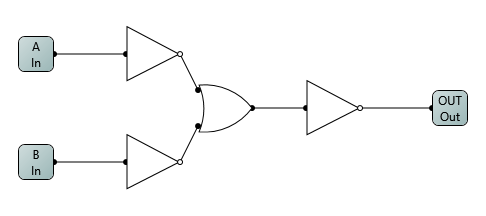
Because of the NOT gate at the end, the NAND gate is just this without it.
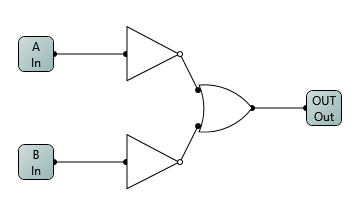
Next, XOR. To start with, I took the basic definition of XOR: exclusive OR, or OR excluding the case where both inputs are true. So, I needed an OR gate, as well as a NAND gate (which is only false when both inputs are true) and then to AND the two. Hence:
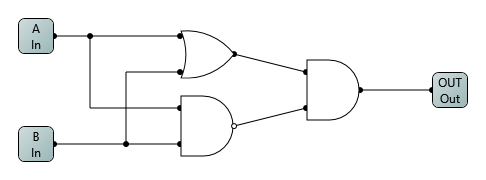
Which is fine, except it isn’t entirely NOTs and ORs, which is sort of the point of what I’m doing. So, I substituted in a NAND and an AND (a new tongue twister!) made from NOT gates.
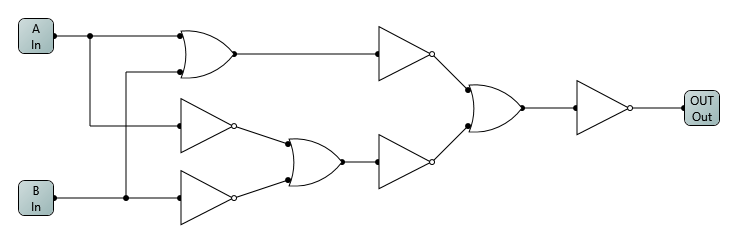
I don’t know if this is the best method, as there’s probably a way to do it that doesn’t translate into other logic gates, but it works.
And again, there’s a NOT on the end so XNOR was easy enough.
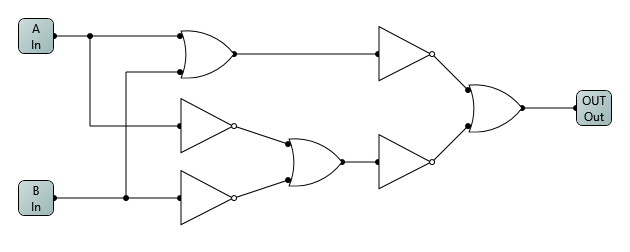
By this point, I was looking for excuses to make as many as I could (I was using a program which I had located just for this and it’s quite great, check out logiccircuit.org) so I made a NOR gate. Why not (no pun intended).
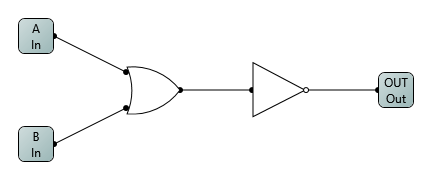
That was tricky. So I moved on to something easier quite harder… a half adder!

(Again, probably a better way, I’d have to stare at the truth table and find something else)
Oooh, but I’m just getting started! How about a full adder?
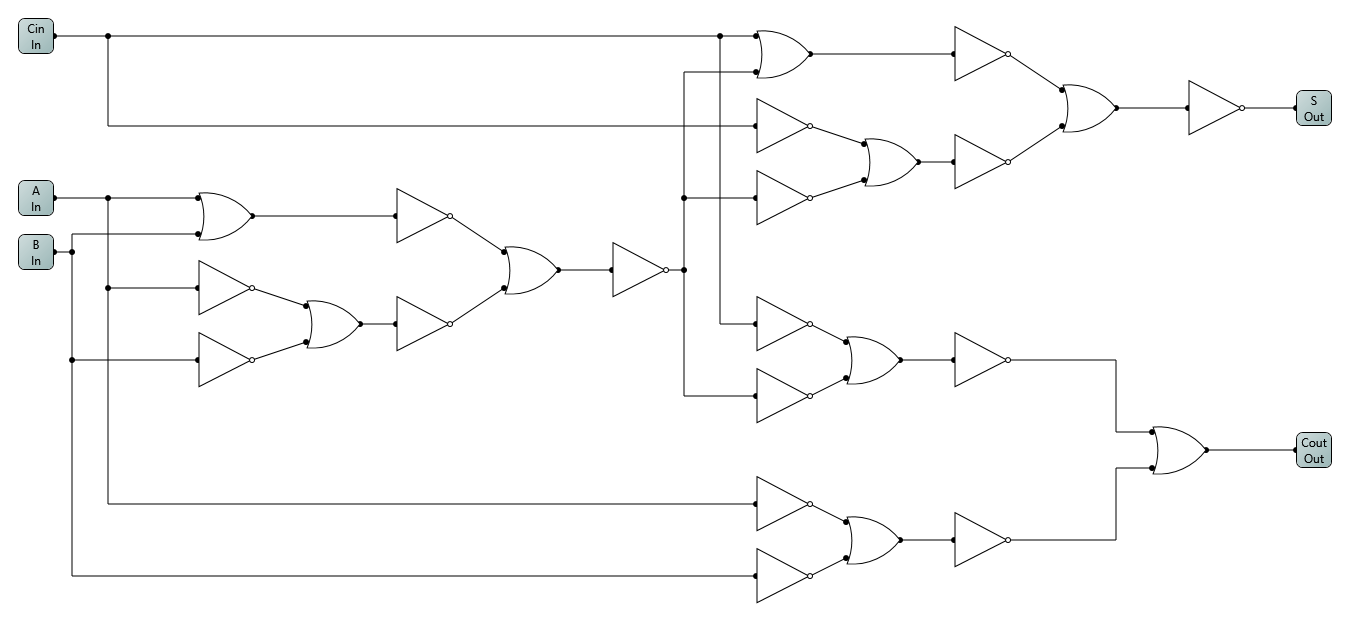
Oh yeah! Now, if I was just getting started, then I think I’m finished now.
How about a 2-bit adder? Maybe another time.
No comments found.