Sorry for the lack of top-notch mathematical formatting, but I’ve done my best to make everything still look good.

0⁰ is an interesting case when it comes to exponents. Whilst anything to the power of 0 is 1, raising 0 to any power gives 0. So what happens when you raise 0 to the power of 0? Is it 0 or 1?

Showing that anything raised to the power of 0 equals one is a fairly trivial matter. From the knowledge that x^a ÷ x^b = x^a-b, it follows that x^a ÷ x^a = x^a-a = x⁰. And since x^a ÷ x^a equals 1, x⁰ must equal 1.

But this doesn’t work if x is 0, because that results in 0^a ÷ 0^a = 0/0, which is either undefined or infinity (depending on your personal opinions).

As far as I can tell, 0⁰ = 1. One of the more intuitive ways of seeing this is to look at the graph of y = x^x.

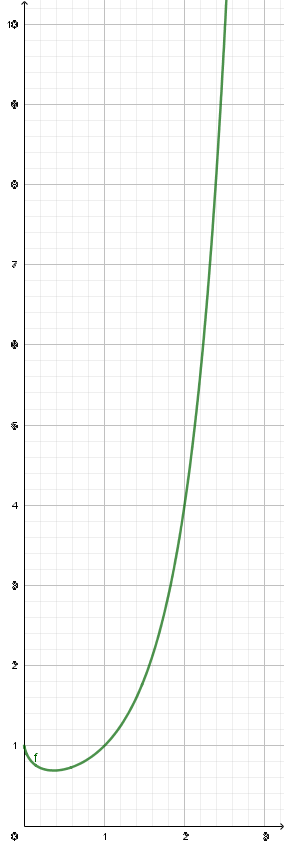
Note how, as x approaches 0, y approaches 0⁰ as well as 1.

 

If this doesn’t convince you, here’s a more formal proof.

The binomial theorem states that (a+b)ⁿ equals the sum of ⁿC_r × a^n-r× bⁿ for r from 0 to n. You might know one particular form of this, that (a+b)² = a² + 2ab + b², however it is technically a²b⁰ + 2a¹b¹ + a⁰b². This leads to something interesting:

If we let a = 1, b = 0, and n = 2, then the left hand side becomes (1+0)² = 1² = 1. But the right hand side becomes 1²×0⁰ + 2×1¹×0¹ + 1⁰×0² and since we know that 0¹ = 0² = 0, it further becomes 1²×0⁰ = 1×0⁰ = 0⁰. And since the left hand side is 1, 0⁰ must be 1.

This works for other values of n, even 0. The left hand side will always simplify to 1, and the right hand side will have every term except 1ⁿ×0⁰ eliminated, as this always becomes just 0⁰.

In the case of n = 0, the left hand is still 1 as (1+0)⁰ = 1⁰ = 1, and  the right hand side becomes simply 1⁰× 0⁰ = 1 × 0⁰ = 0⁰.

From this it seem logical to conclude that 0⁰ must be equal to 1.

There might be equations that only work if 0⁰ has some other value, but I don’t believe I’ve encountered a situation like that. If you know of one, don’t hesitate to mention it in the comments.