For the most part, everything to do with orbits is a consequence of one simple rule: Newton’s law of universal gravitation. It simply states that all masses are attracted by a force that increases with mass and decreases faster with distance. General relativity describes certain physical observations much more accurately, but the differences only become significant under more extreme circumstances that don’t typically come up in the context of our solar system, so it will not be discussed here.
So, given the positions and masses of a bunch of objects, it’s possible (and quite easy) to determine what force (and thus acceleration) acts on each. Problem solved, right?
Kepler orbits
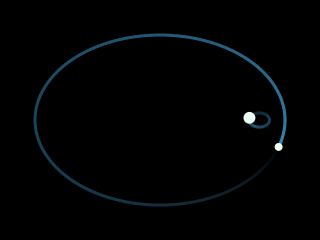
In the case of two objects: yes! The motion of each can be described by a Kepler orbit, the trajectory that results when the only force acting on an object is the gravitational pull of one other.
The equations involved are slightly more complicated, especially those for determining the actual orbit from position and velocity, but they are regardless well-known and universal.
However, the universe is not two point masses.
Numerical solutions
Solving for the motion of more than two bodies is not simple. Doing so is called the n-body problem and it remains just that: a problem. Without making any assumptions about the nature of the system, it is simply not possible to fully describe the motions of each body.
But back to basics: the forces are known. From force, acceleration can be found. From that, velocity. And from that, the end goal: positions. All that’s required is integration!
Only problem is, there’s no actual expression for acceleration, nor velocity, to integrate. All that’s known is the accelerations at a single point in time.
Fortunately, there are methods to approximate how velocities and thus positions will change over a certain period of time, referred to as numerical integration. These are a whole other subject of their own, but the basic aspect is they can approximate the state of the system some time in the future based on its current state. Their accuracy under myriad circumstances varies widely, but in general a smaller timestep will produce less error.
Velocity Verlet integration is a good choice for orbits, as it explicitly incorporates both position and velocity, and works well when acceleration is a continuous function of position (as it is with gravity).
What to use?
At this point it might seem pretty clear that a numerical solution is required for almost anything. In fact, it’s actually easier to implement because there are very few formulae and they’re all pretty simple.
But there is a significant downside when it comes to real-time simulation: in order to determine the state of the system at any point in the future, it is necessary to integrate many small steps to get there. On the scale of planets and moons you might be able to get away with steps of 1000 seconds without accumulating any significant error, but that’s still upwards of 30000 steps to advance by just one year (which is not very much when discussing orbits).
And it gets worse: if there is just one Low Earth Orbit satellite present, the entire simulation is limited to at most 20 seconds at a time to maintain its stability. So in the same simulation, just that one satellite will make a separate trip to Jupiter require a few million simulation steps.
But, we already know that satellite is in a stable orbit. Does it really need to simulated so precisely?
Patched conic approximation
A typical system is not very chaotic. There aren’t three or more similar-mass objects in close proximity all interfering with each other in unpredictable ways. So a patched conic approximation makes two assumptions: every object is being predominantly affected by only one body at a time, and does not affect that body in any significant way itself.
That reduces the entire system to a dozen or so two-body problems; really just a one-body problem in practice due to the one-way interactions. And those interactions have already been solved. In a patched conic approximation, every body has a sphere of influence, and everything inside that sphere of influence follows a Kepler orbit around it. Now it’s possible to jump ahead huge amounts of time, no matter how large or small an orbit might be.
There is one caveat: it’s not fully accurate to advance every single object by ten millenia at once, because objects can cross into other bodies’ spheres of influence. For instance, if something crosses the orbit of the moon, eventually it might get close enough that it would have to transition to a moon-centred orbit, and then exit again onto a different Earth-centred orbit. So it is still necessary to make somewhat-smaller steps, but they can regardless be much larger than would be required with a numerical solution.
But note that in the case that this intercept is skipped over, the stability of the simulation will be completely unaffected. That object will not be following the path it should have been, however it will still be on a fully valid trajectory.
Downsides to patched conics
A patched conic approximation is not completely accurate. Close, circular orbits are generally pretty stable, but in reality the effects of multiple bodies result in all sorts of interesting phenomena like precession, Lagrangian points and trojans, and other perturbations in general. And these perturbations aren’t always in the scale of hundreds of years; although natural satellites have all settled into relatively stable orbits, anything led into a high orbit or a path that comes close to another moon will experience significant alterations to its trajectory.
Summation
What works well is to use patched conics for natural satellites, then do numerical integration on additional objects if that can be done quickly enough, reverting to patched conics otherwise. The paths of natural satellites can be made even more accurate by using an ephemeris: the result of a highly-accurate computer simulation that gives a more complicated but more accurate path for a body over a specific range of time.
If you would like to see what sort of results numerical integration can yield, you might be interested in an orbit simulation I’ve been writing which does just that. Move into an orbit close to – but still below – that of the moon, for instance, and you should note it getting bumped around a bit.
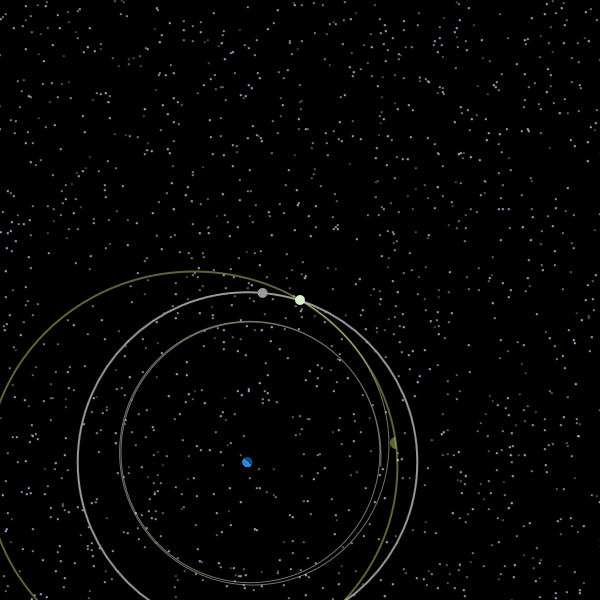
The moon has pulled me out of a stable orbit 
onto an escape trajectory 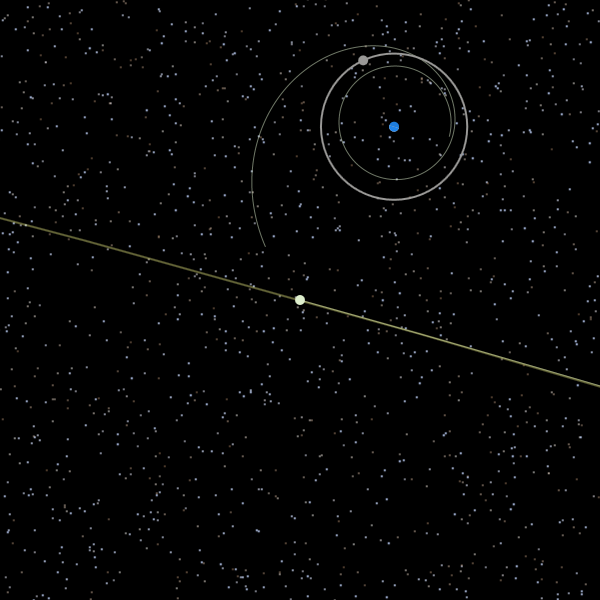
and around the sun
No comments found.